The Y-combinator

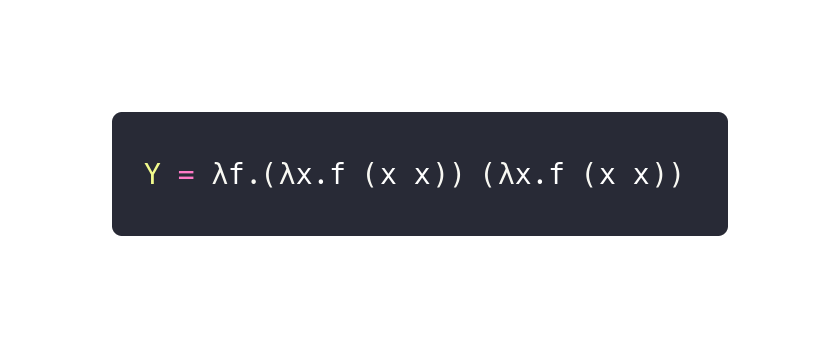
There is a question, how do we have a recursive function expressed using lambda calculus expression.

For example, a factorial function, is typically defined as:

let f = \x . (x > 0) ? x * f(x-1) : 1

In this form of definition. Observed that the expression refer to itself
by its name.

What we want to is to have a anonymous function defined using lambda expresion
only, without depending the name of the function out side.

So how can we achieved that:

First attempt

If we could refer to the factorial f by passing it as a argument to the function.

let F = \ f x . (x > 0) ? x * f(x-1) : 1

Now, we have a function F, which takes a desired function f
(here is the factorial function) as it first parameter,
so that we could have the factorial function refer to itself using this
argument.

But here comes the problem, we have to supply f in order to define f.

let f = F(f)

The problem is not solved.
In order to define f without f itself.
Assume there exists a function Y that do such magic transform,
turn the function F into f.

So we have:

let f = F(f) = Y(F)

Now the problem becomes, how do we find a function Y, if Y is found,
then the problem is solved.

In fact, this Y function does exists, whose name is Y-combinator

Second attempt

Recall that we want to define f anonymously, without referring to symbols outside.

In previous attempt, we trying to pass the desired function f as the argument in to a
function F, then using the origin function f to define it.

How about, instead of passing the desired function f as argument, we could pass the
function g, where the function g take itself g as the first argument, and follow
with a normal argument x same as that is passing to f as the second one.

We have:

let g = \g x . (x>0) ? g(g)(x-1)*x : 1

Luckily, since the function g itself take it self as first argument.
We could simply compose two g function to form f, which exactly forms the
function we want. Without dependencies.

let f = g(g)
      = (\g . g(g))(\g x . (x>0) ? g(g)(x-1)*x : 1)
      = (\g x . (x>0) ? g(g)(x-1)*x : 1)(\g x . (x>0) ? g(g)(x-1)*x : 1)

Now we get the desired factorial defined anonymous lambda function.

Done !?

No if you think composing two g as f,

Back to first attempt

Now we know how to define f using g, this give us clues to solve Y.

As we already known, the f could be defined by composing using two g.

If g is expressed and defined using F, then f could be expressing using F.

We know:

f = g(g) = Y(f) = F(f)

Expressing g using F. Remember that g is a function take itself as parameter.

let g = \g . F(g(g))

Then we know how to express f using F

let f = g(g) = (\g . F(g(g)))(\g . F(g(g)))

Now we know how to define the Y-combinator.

let Y = \f . F(f) = \f . F((\g . F(g(g)))(\g . F(g(g))))

The Y-combinator

Hooray !! The Y combinator is born. Now we could easily define our
recursive function using Y-combinator

factorial = Y(\f x . (x>0) ? (x)*f(x-1) : x)